【机器学习-17】数据变换---小波变换特征提取及应用案列介绍

04-27 1491阅读 0评论

引言

在机器学习领域，数据变换是一种常见且重要的预处理步骤。通过对原始数据进行变换，我们可以提取出更有意义的特征，提高模型的性能。在众多数据变换方法中，小波变换是一种非常有效的方法，尤其适用于处理非平稳信号和时频分析。本文将详细介绍小波变换的数学原理及其在特征提取中的应用。

一、小波变换的介绍

小波变换作为一种前沿的数据分析工具，近年来在信号分析领域崭露头角。小波分析的理论和方法凭借其独特优势，在信号处理、图像处理、语音处理、模式识别以及量子物理等多个领域得到了广泛的应用，堪称近年来在工具及方法上的重大突破。小波变换以其多分辨率的特性，在时域和频域均展现出对信号局部特征的强大表征能力。通过伸缩和平移等运算过程，小波变换能够对信号进行多尺度聚焦分析，为非平稳信号的时频分析提供了一种有效手段。它允许我们由粗及细地逐步观察信号，从而精准地提取出有用信息。

小波变换作为一种信号分析方法，其核心思想在于将信号分解为一系列小波函数的叠加。小波函数是一类具有有限支撑集、在正负之间振荡的波形，其特性使得小波变换能够在时域和频域同时提供局部化信息，从而更加适用于非平稳信号的处理。在实际问题中，特征量往往隐含在信号的某个或某些分量中，小波变换通过分解非平稳信号为表达不同层次、不同频带信息的数据序列，即小波系数，从而实现对信号的特征提取。

具体而言，小波变换的基本思想涉及信号与小波函数的内积运算。这一运算过程能够生成不同尺度下的小波系数，这些系数反映了信号在不同尺度和位置上的特征。通过精心选择小波函数和尺度参数，我们能够对信号进行多尺度分析，深入揭示信号中隐藏的结构信息。这一特性使得小波变换在信号分析领域具有独特的优势，为信号处理提供了新的视角和工具。

二、基于小波变换的特征提取方法 [ 1 ] ^{[1]} [1]

基于小波变换的特征提取方法主要有:基于小波变换的多尺度空间能量分布特征提基于小波变换的多尺度空间的模极大值特征提取、基于小波包变换的特征提取、基于适应性小波神经网络的特征提取，详见下表：

基于小波变换的特征提取方法 \bold{基于小波变换的特征提取方法} 基于小波变换的特征提取方法

基于小波变换的特征提取方法	方法描述
基于小波变换的多尺度空间能量分布特征提取方法	各尺度空间内的平滑信号和细节信号能提供原始信号的时频局域信息，特别是能提供不同频段上信号的构成信息。把不同分解尺度上信号的能量求解出来，就可以将这些能量尺度顺序排列，形成特征向量供识别用
基于小波变换的多尺度空间的模极大值特征提取方法	利用小波变换的信号局域化分析能力，求解小波变换的模极大值特性来检测信号的局部奇异性，将小波变换模极大值的尺度参数s、平移参数及其幅值作为目标的特征量
基于小波包变换的特征提取方法	利用小波分解，可将时域随机信号序列映射为尺度域各子空间内的随机系数序列，按小波包分解得到的最佳子空间内随机系数序列的不确定性程度最低，将最佳子空间的熵值及最佳子空间在完整二叉树中的位置参数作为特征量，可以用于目标识别
基于适应性小波神经网络的特征提取方法	基于适应性小波神经网络的特征提取方法可以把信号通过分析小波拟合表示，进行特征提取

在机器学习中，特征提取是一个关键步骤。通过特征提取，我们可以从原始数据中提取出有意义的特征，为模型训练提供有力的支持。小波变换作为一种有效的数据变换方法，可以用于特征提取。

基于小波变换的特征提取通常包括以下步骤：

选择合适的小波函数和尺度参数。不同的小波函数和尺度参数会对特征提取结果产生不同的影响。因此，在实际应用中，我们需要根据具体任务和数据特点选择合适的小波函数和尺度参数。
对原始信号进行小波变换。通过计算信号与小波函数的内积，得到不同尺度下的小波系数。
提取小波系数作为特征。根据任务需求，我们可以选择部分或全部小波系数作为特征。这些特征可以用于后续的机器学习模型训练。
对特征进行进一步处理。为了提高模型的性能，我们可以对提取出的小波系数进行进一步处理，如降维、归一化等。

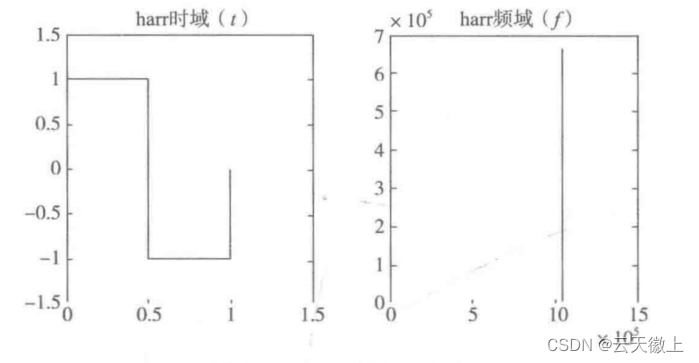
2.1 小波基函数

小波基函数是一种具有局部支集的函数，并且平均值为0，小波基函数满足 ψ ( 0 ) = ∫ ψ ( t ) d t \psi(0)= \begin{aligned} \int \psi(t) \mathrm{d} t \end{aligned} ψ(0)=∫ψ(t)dt常用的小波基有Haar小波基、db系列小波基等。Haar小波函数如下图所示。

2.2 小波变换

对小波基函数进行伸缩和平移变换:
ψ a , b ( t ) = 1 ∣ a ∣ ψ ( t − τ a ) \psi_{a,b}(t) = \frac{1}{\sqrt{|a|}} \psi(\frac{t-\tau}{a}) ψa,b(t)=∣a∣ 1ψ(at−τ)
其中， a a a为伸缩因子， τ \tau τ为平移因子。
任意函数 f ( t ) f(t) f(t)的连续小波变换（CWT）为：
W f ( a , b ) = ∣ a ∣ − 1 / 2 ∫ f ( t ) ψ ( t − τ a ) d t W_f(a,b)=|a|^{-1/2}\begin{aligned} \int f(t) \psi(\frac{t-\tau}{a}) \mathrm{d} t \end{aligned} Wf(a,b)=∣a∣−1/2∫f(t)ψ(at−τ)dt
可知，连续小波变换为 f ( t ) → W f ( a , τ ) f(t) \rightarrow W_f(a,\tau) f(t)→Wf(a,τ)的映射，对小波基函数 ψ ( t ) \psi(t) ψ(t)增加约束条件 C ψ = ∫ ∣ ψ ( t ) ^ ∣ 2 t d t