MATLAB R2021b--求解常微分方程
记录常微分方程MATLAB解法的学习
目录
一·连续系统的数学建模方法
(一)连续系统
1.微分方程模型
2.传递函数模型
3.状态空间模型
(二)微分方程建模
微分方程的机理建模法(解析法)
二·常微分方程的数值解法
1.微分方程
2.常用方法
(1)欧拉法
从导数的角度理解欧拉公式:
欧拉法的应用:
从数值积分角度理解欧拉公式:
(2)改进的欧拉法
改进的欧拉法的应用:
(3)龙格-库塔法(Runger-Kutta法)
局部截断误差和阶
标准(经典)四阶龙格-库塔法:
龙格-库塔法的应用:
(4)亚当姆斯法
线性多步法的概念:
3.一阶常微分方程组的数值解法
4.高阶常微分方程的数值解法
三·MATLAB求解常微分方程
(一)解析解
1.dsolve
(二)数值解
1.solver
编辑
2.高阶常微分方程
(三)综合实例
1.一阶微分方程
(1)将方程写成函数文件
(2)解析解
(3) 求解器法
(4)欧拉法
(5)改进欧拉法
(6)龙格-库塔法
结果:
2.二阶微分方程
(1)把方程写成函数文件
(2)解析解
(3)欧拉法
(4)改进欧拉法
(5)龙格-库塔法
(6)求解器
结果:
一·连续系统的数学建模方法
(一)连续系统
连续系统是指系统的状态变量随着时间连续变化的系统,可通过常微分方程或偏微分方程来描述。
常用的连续系统数学模型有: 微分方程模型 ,传递函数模型 , 状态空间模型。
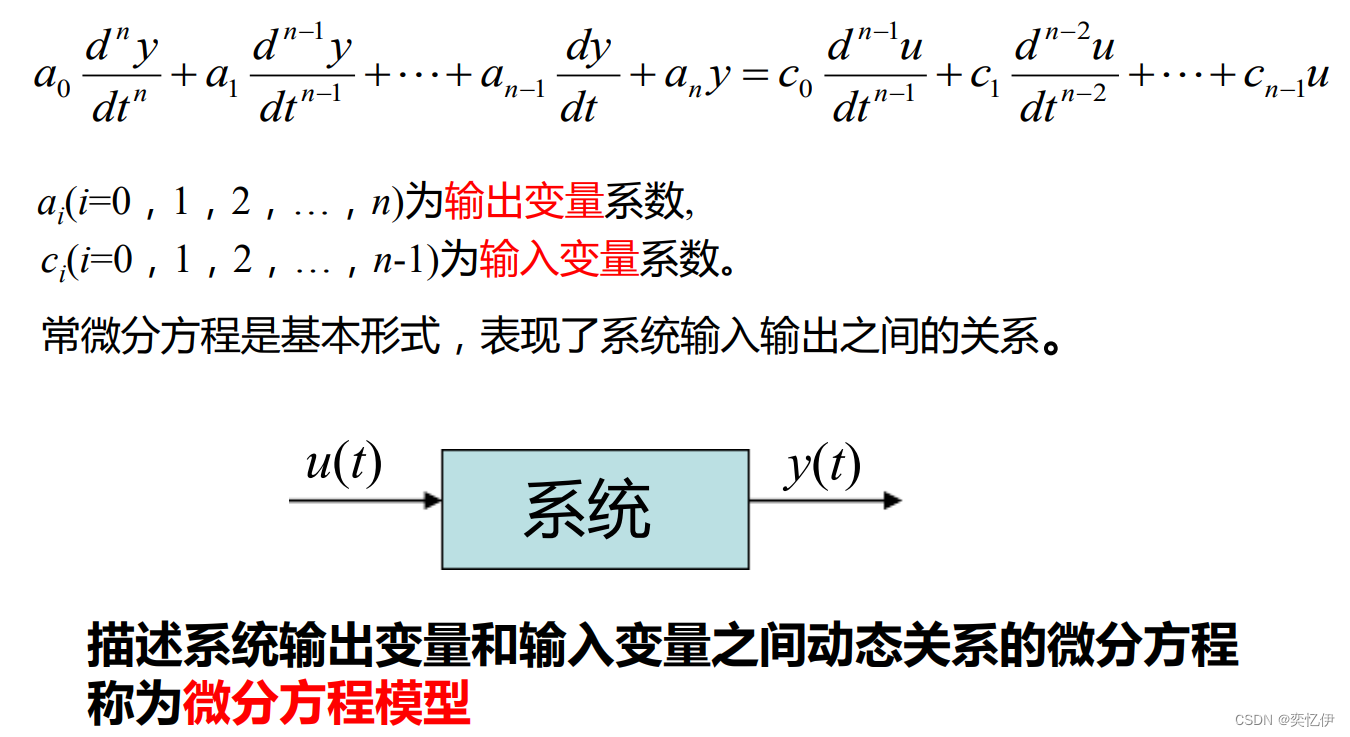
1.微分方程模型
2.传递函数模型
3.状态空间模型
由微分方程可以导出系统的传递函数和状态方程等多种数学模型。 因此,建立系统的微分方程是建模技术中的重要内容。
(二)微分方程建模
微分方程的机理建模法(解析法)
(1)使用前提:该方法是依据基本的物理、化学等定律,进行机理分析,确定模型结构、参数; 使用该方法的前提是对系统的运行机理完全清楚。
(2)基本原理:机理建模法又称为直接分析法或解析法,是应用最广泛的一种建模方法,一般是在若干简化假设条件下,以各学科专业知识为基础, 通过分析变量间的关系和规律,而获得解析型数学模型。
(3)建模步骤:
① 分析系统功能、原理,对系统做出与建模目标相关的描述 (系统原理图);
② 找出系统的输入变量和输出变量;
③ 按照系统(部件、元件)遵循的内在规律(物化、生态、经济 规律),列写
出各部分的微分方程,建立微分方程组。
④ 消去中间变量,导出只含有输入、输出量的微分方程;
⑤ 标准化微分方程,将输出各项移到方程左侧,输入各项移到方程右侧,各阶导数项
按阶次从高到低的顺序排列。
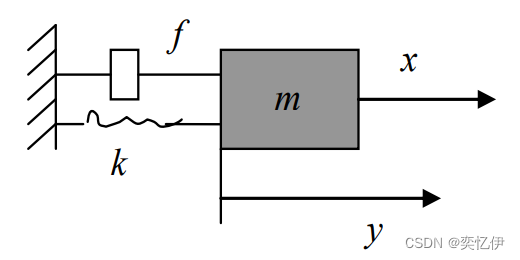
例1.1:机械平移系统
这是一个由阻尼器,弹簧,物体构成的系统。f是阻尼器的阻尼系数,k是弹簧的弹性系数。
输入:外力x
输出:物体的位移y
设阻尼器施加给物体的力为 x1,弹簧施加给物体的力为 x2
根据牛顿第二定律列方程:
消去中间变量 x1,x2
标准化微分方程:
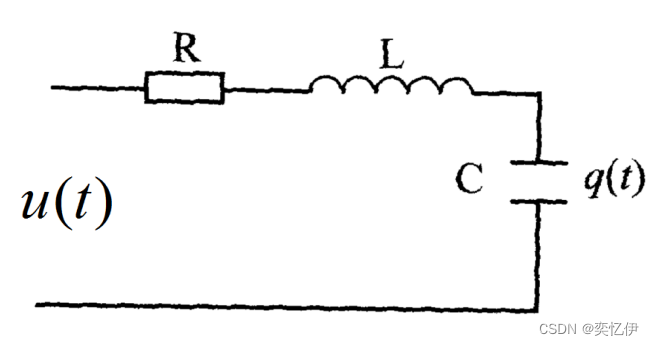
例1.2 :R-L-C电路
输入:电压u(t)
输出:电量q(t)
设电阻R上的电压为 uR,电感L上的电压为 uL,电容C上的电压为 uC
根据基尔霍夫电压定律列方程:
消去中间变量:
标准化微分方程:
以上推出的各种系统的运动方程(数学模型),尽管它们的物理模型不同,却可能具有相同的数学模型,这种具有相同的微分形式的系统称为相似系统。将作用相同(在微分方程中占据相同位置) 的物理量称为相似量。
比较两个例子可以看出它们具有相同的数学模型,是相似系统。
小结一下:
二·常微分方程的数值解法
1.微分方程
在许多实际问题中,往往不能完全清楚系统机理直接写出函数的解析表达式,但根据已知条件,有时可列出含有待求函数及其导数的关系式——微分方程。
以上两个例子抽象出来实际上就是一阶微分方程的初值问题:
实际上,只有少数问题如 例2.1 例2.2 能求出y(x)的解析表达式,对大多数微分方程要求出函数的准确表达式,计算量大、甚至不可能,但是实用上有时只需得到在某些点处的函数近似值即可。
求yk的离散化方法:欧拉法,改进欧拉法,龙格-库塔法,亚当姆斯法。
下面对这几种方法做简单介绍
这里不做过多的数学深究,只在于运用。
2.常用方法
(1)欧拉法
从导数的角度理解欧拉公式:
①向前差商
我们知道导数可以近似为差商的形式:
令:
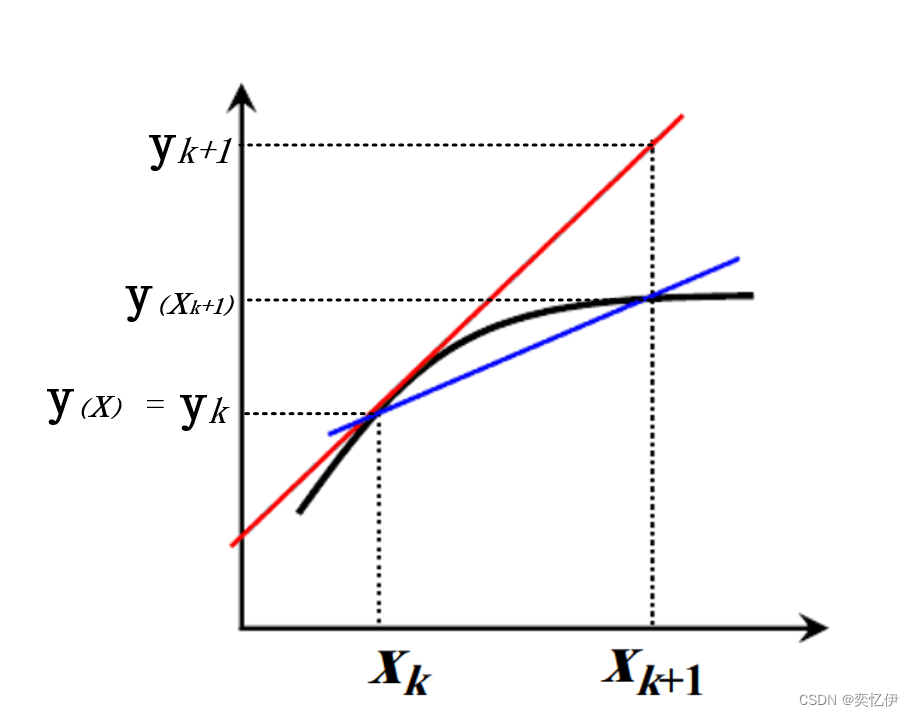
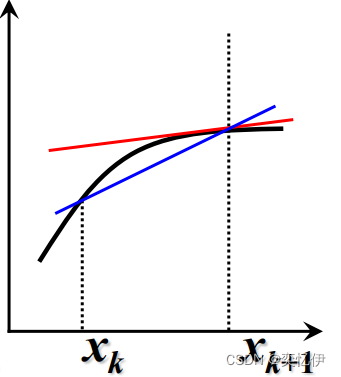
图示如下:yk+1与y(xk+1)不同,前者是近似值后者是实际值,而初值yk与y(xk)相等
将Ⅱ式带入Ⅰ式得到欧拉公式:
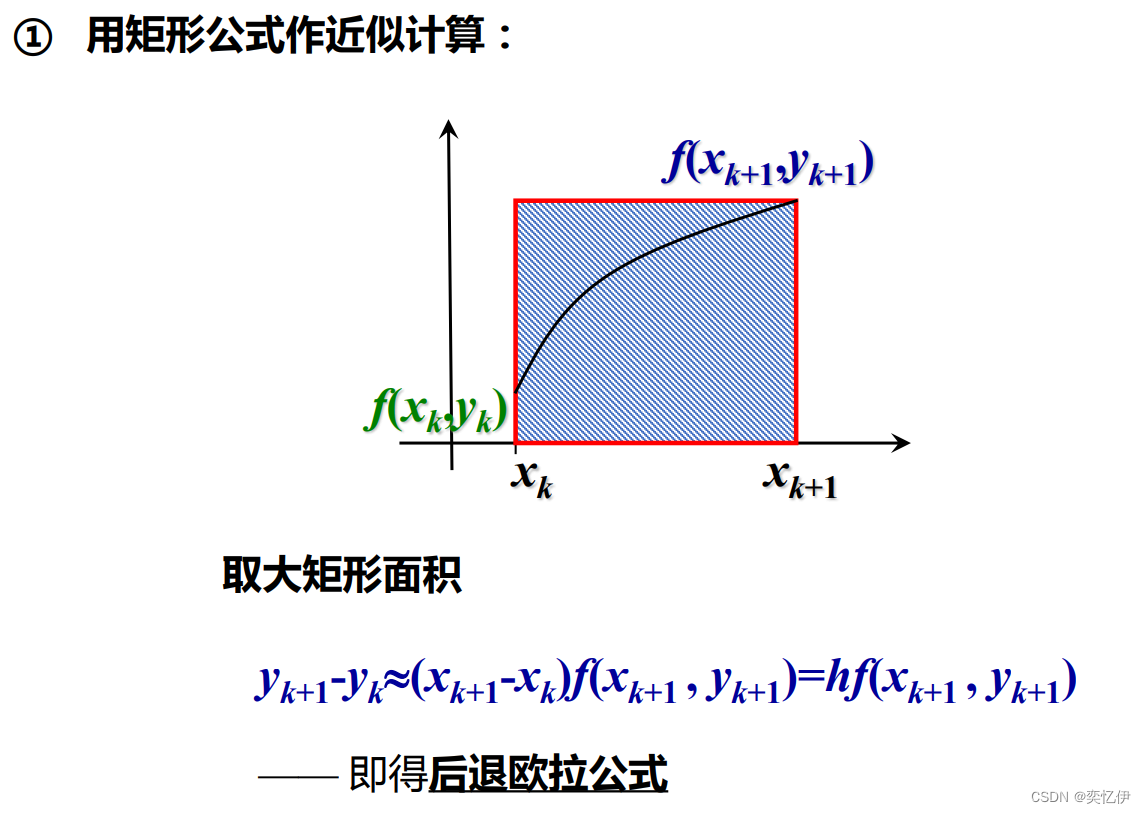
②向后差商
令:
图示如下:
同理,得到后退欧拉公式:
③中心差商
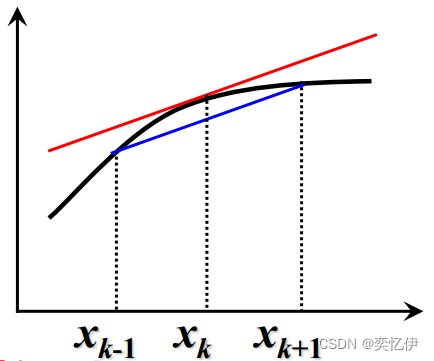
同理,得到中点欧拉公式:
图示如下:
其实我们常用的是一般的欧拉公式
公式:
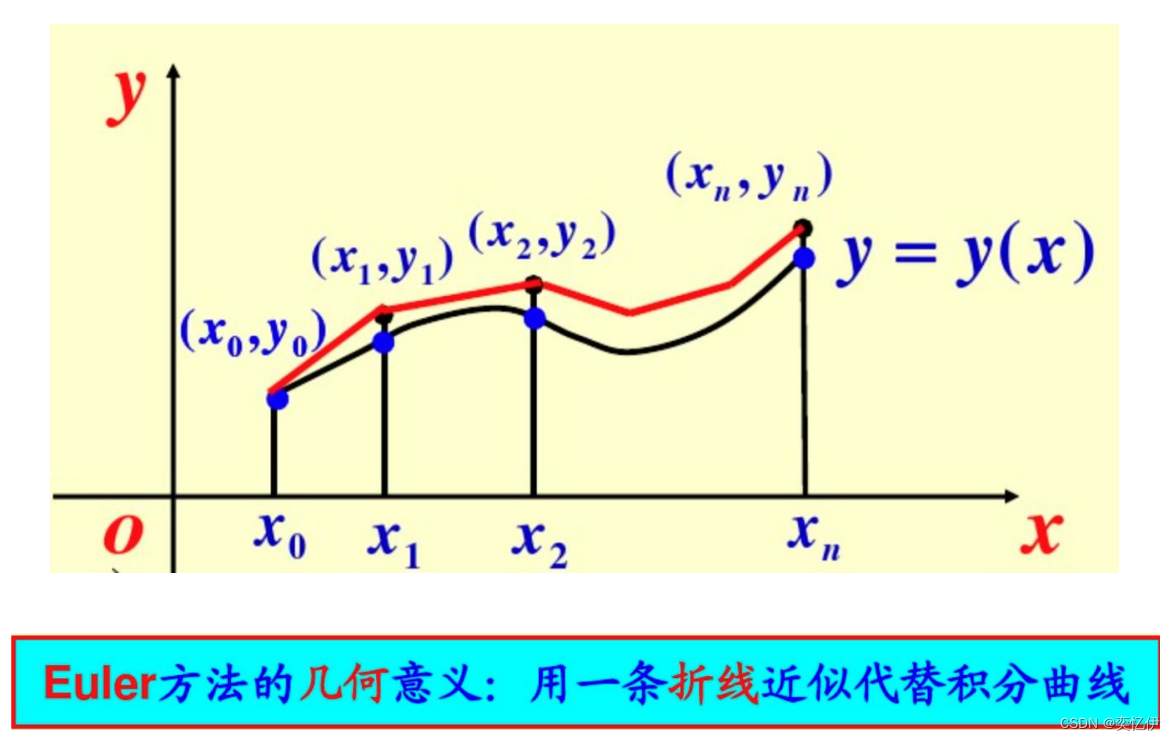
以此类推可以得到欧拉法的几何意义:
欧拉法也称 欧拉折线法
注意:“折线法” 而非“切线法” 除第一个点是曲线切线外,其他点均不是
欧拉法的应用:
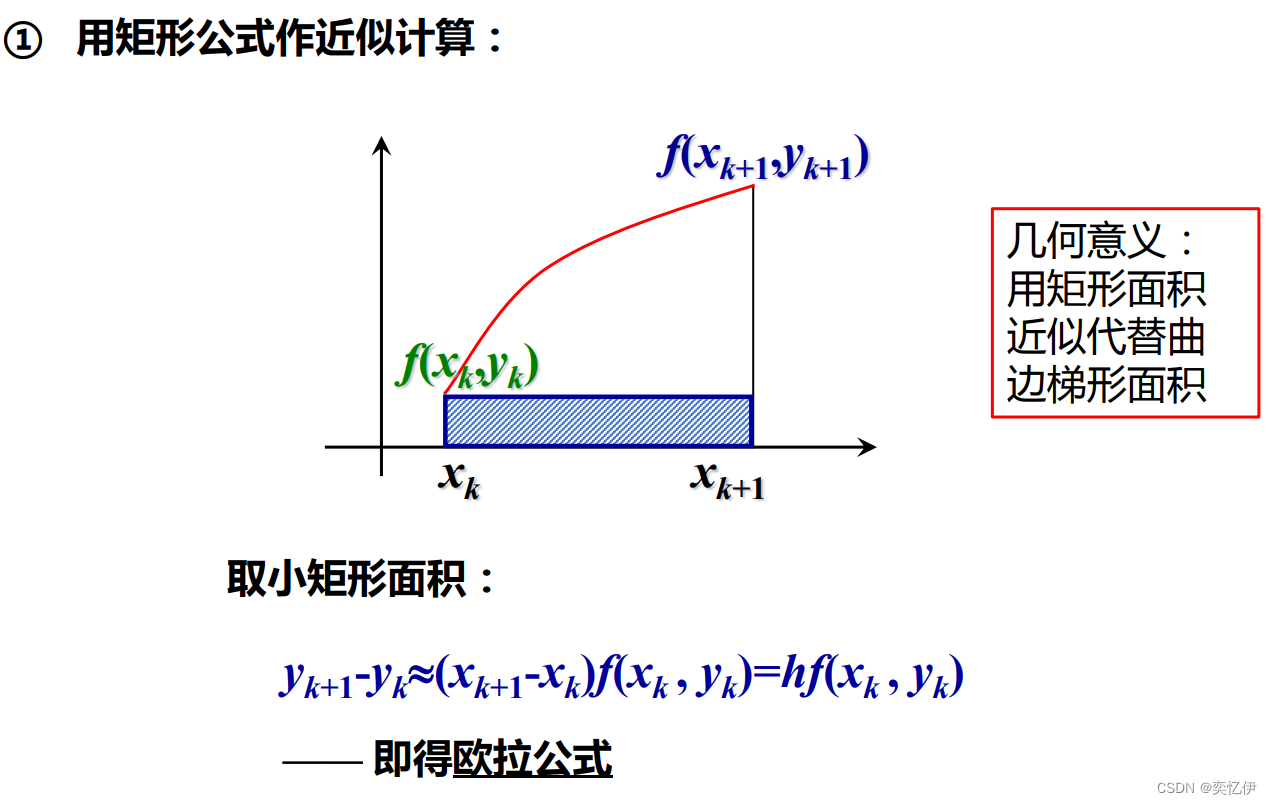
除了从微分(导数)的角度推出欧拉公式外,我们还可以从积分的角度推公式。
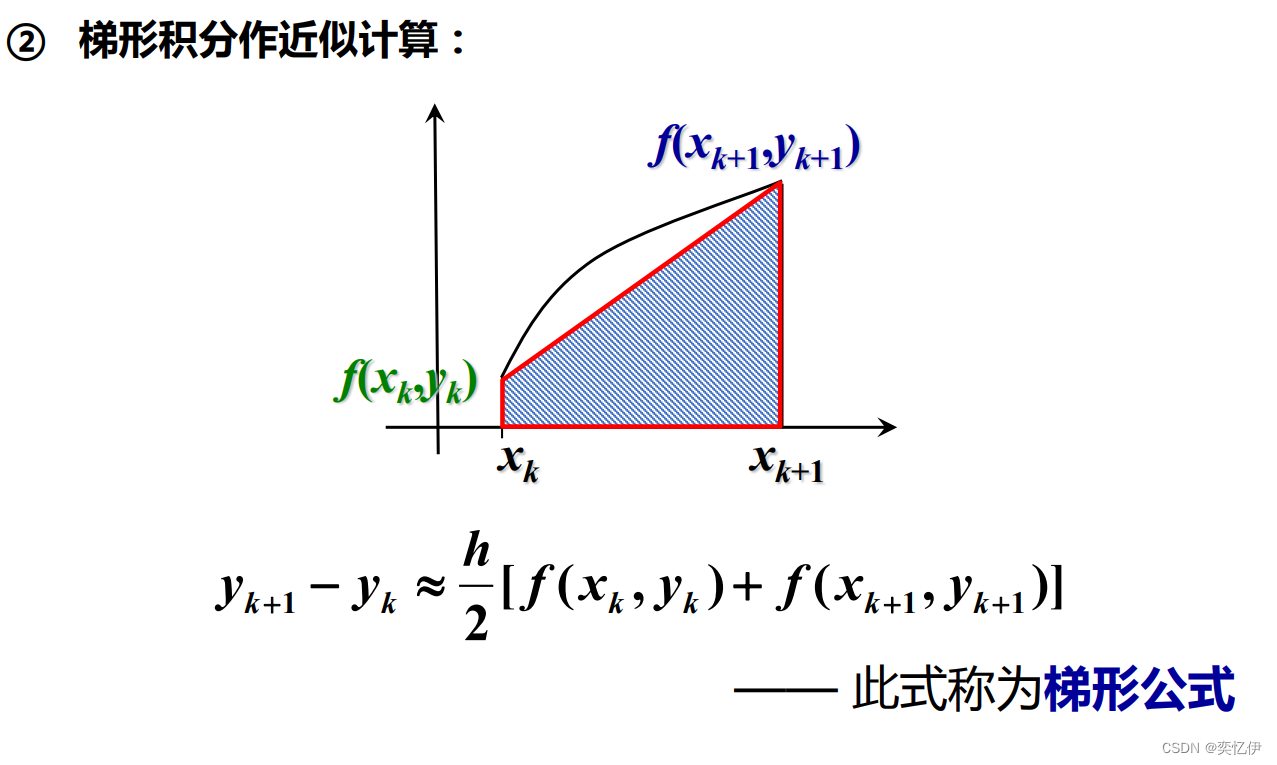
从数值积分角度理解欧拉公式:
在梯形公式中,计算yk+1时,计算式中含有未知的yk+1,这样的公式称为隐式公式。
(2)改进的欧拉法
将梯形公式和欧拉公式结合使用,先用欧拉公式由已知的初值计算第一次yk+1,然后把初值和第一次计算的yk+1代入梯形公式计算修正后的yk+1
两个公式组合如下:
此公式也称为预估-校正公式。
预估---由欧拉公式求第一次yk+1的过程;
校正---代入梯形公式迭代计算第二次yk+1的过程。
用预估-校正公式求解常微分方程的方法即为——改进的欧拉法。
此公式可以改写为
改进的欧拉法的应用:
(3)龙格-库塔法(Runger-Kutta法)
使用泰勒公式也可以推导欧拉法和改进的欧拉法,这里主要是为了引出龙格-库塔法的推导。
插播一下 。。。。。。
局部截断误差和阶
这里需要了解误差分析中,局部截断误差和阶的概念
设yn是准确的,用某种方法计算yn+1时产生截断误差 实际上yn不是准确的,因此它的误差会传播下去。 实际计算时,每一步都可能产生舍入误差。
知道概念后可以得到欧拉公式的局部截断误差和阶
同理,改进欧拉公式取到泰勒的二阶展开式,局部截断误差为三阶,公式是二阶。
小结一下:
结论:计算几次K(f),公式就是几阶
局部截断误差比公式高1阶
龙格-库塔法就是按照上述的思想构造
从几何意义上看,欧拉法是用斜率f(xn ,yn )逼近,而龙格-库塔法则是 可以看成用p个斜率
Kr=f(xr ,yr )的一种加权平均逼近,因此能够提供计算精度。
采用类似二阶龙格-库塔法的构造方法,即可得三阶龙格-库塔法 (截断误差为O(h^4 ))和四阶龙格-库塔法(截断误差为O(h^5 ))。
标准(经典)四阶龙格-库塔法:
龙格-库塔法的应用:
(4)亚当姆斯法
单步法:从x0开始,逐步求取x1,x2,...,xn处的函数 值近似值y1,y2,...,yn,求yn+1时要用到前一步结果yn。(改进的欧拉法)
两步法:每前进1步,即求yn+1时要用到前2步结果yn-1和yn。(中点欧拉公式)
单步法优点: 原理简单并可根据需要调整步长大小;
单步法缺点: 要得到高精度解,计算量大。 如四阶龙格-库塔法,每前进一步(求yn+1)需计算4次f(x,y)函数值。
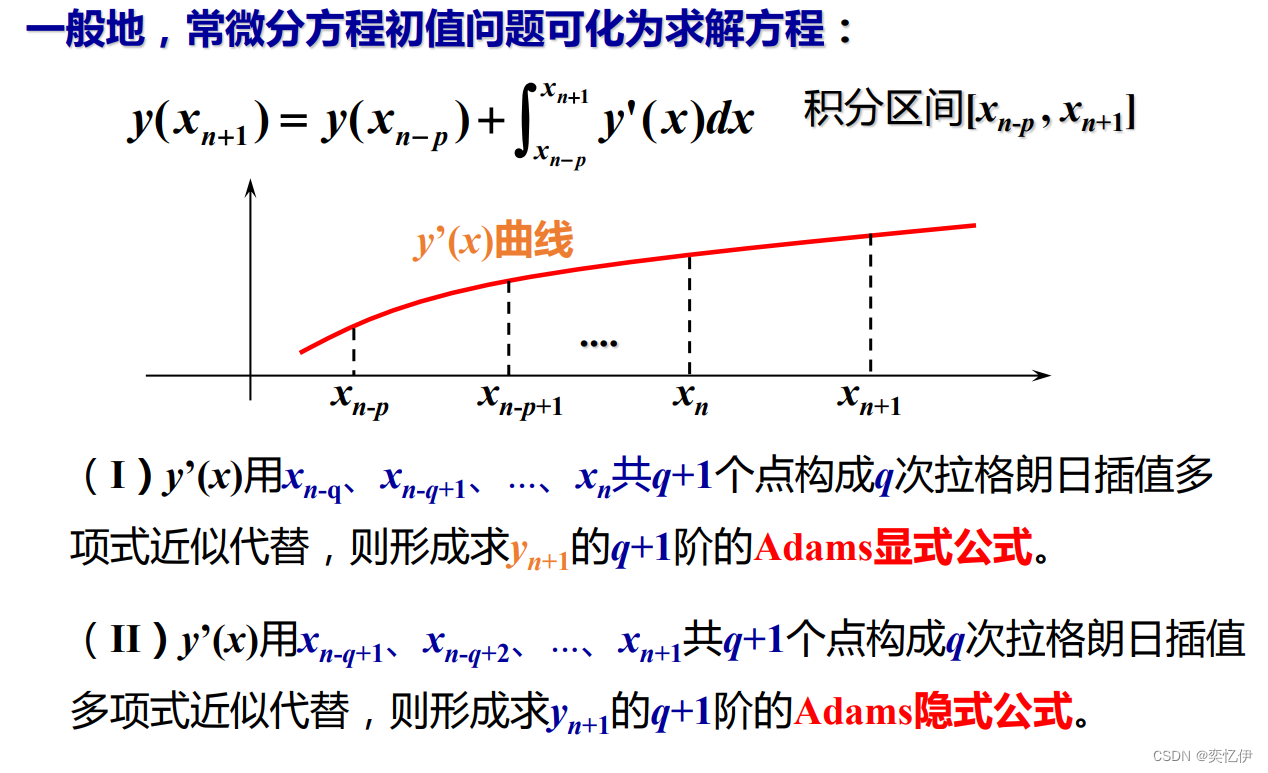
亚当姆斯法属于线性多步法
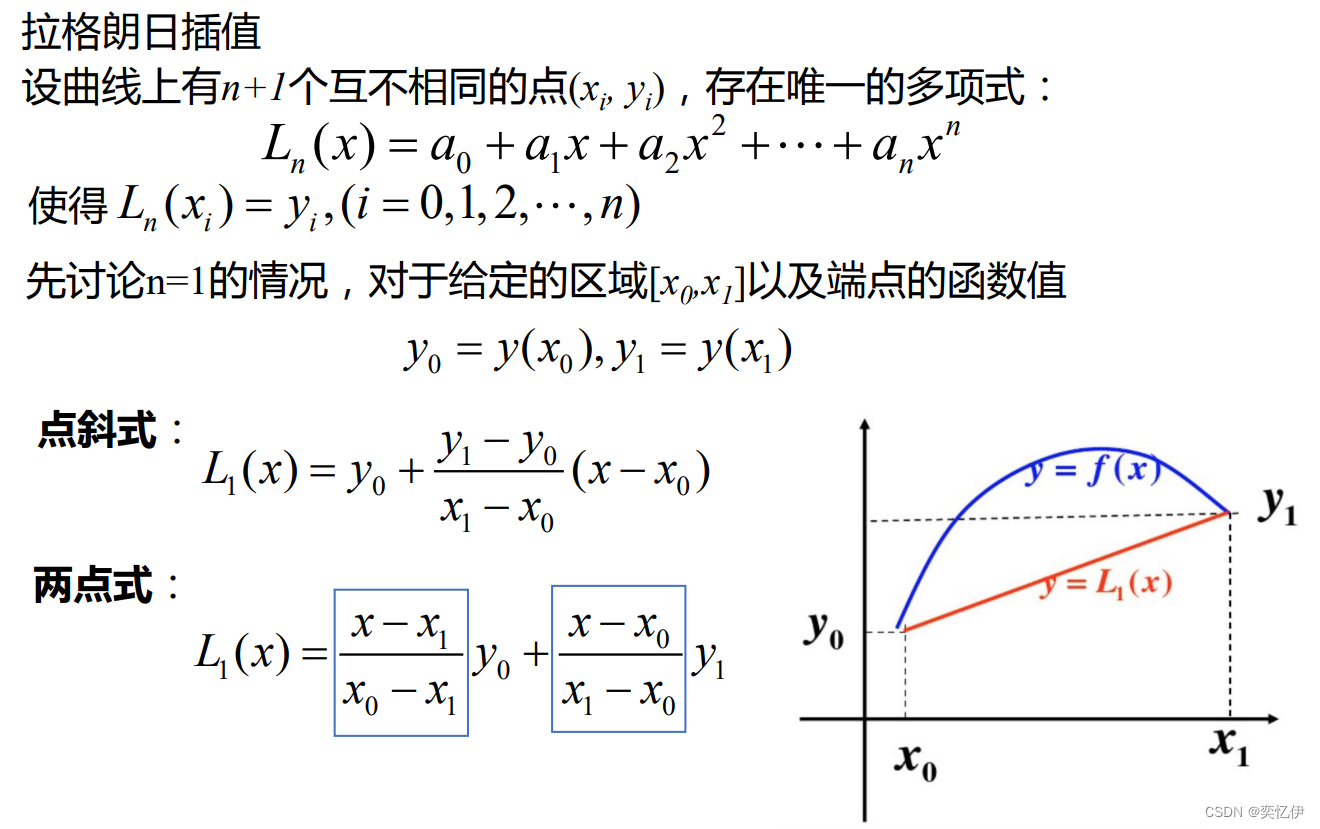
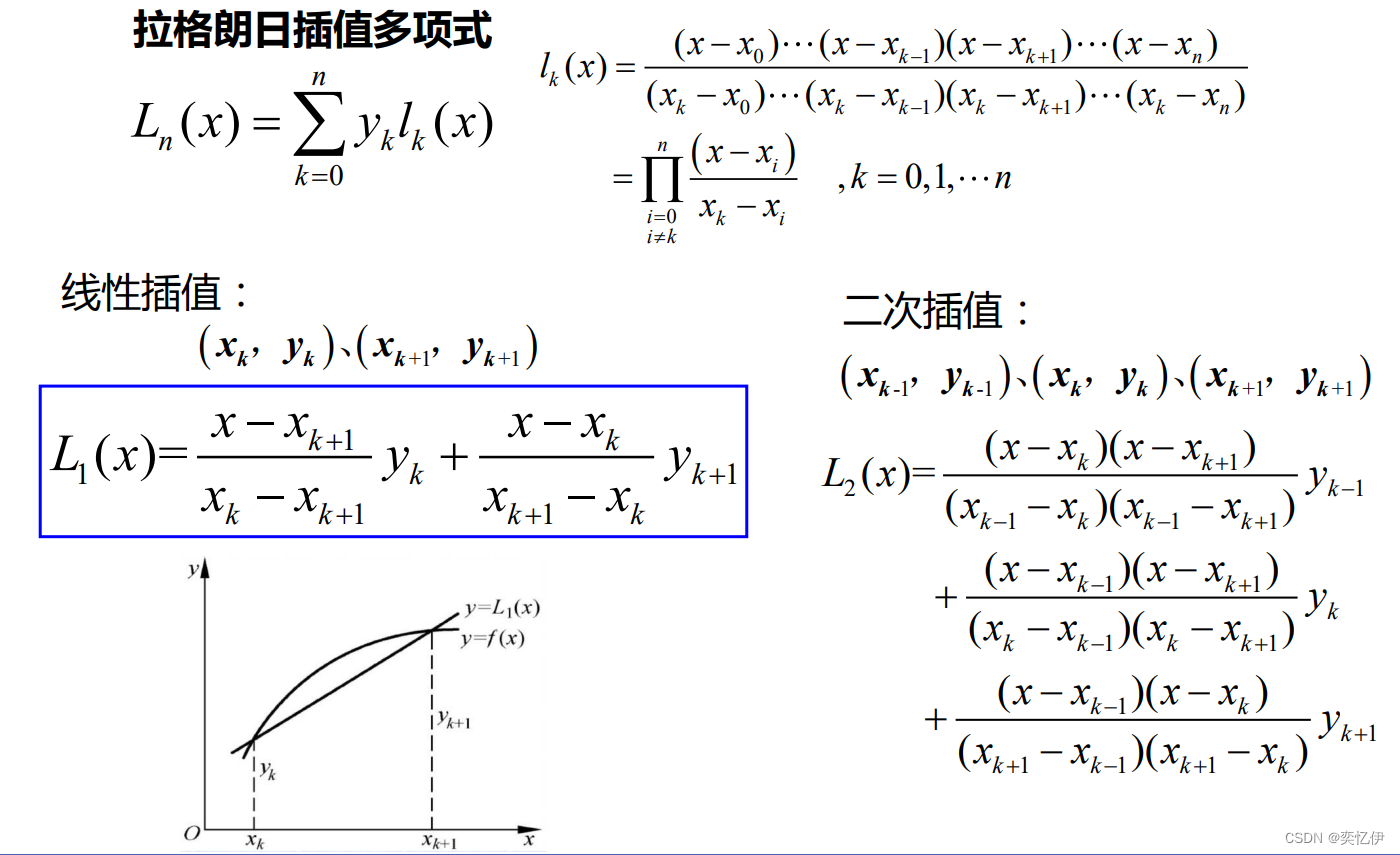
线性多步法的概念:
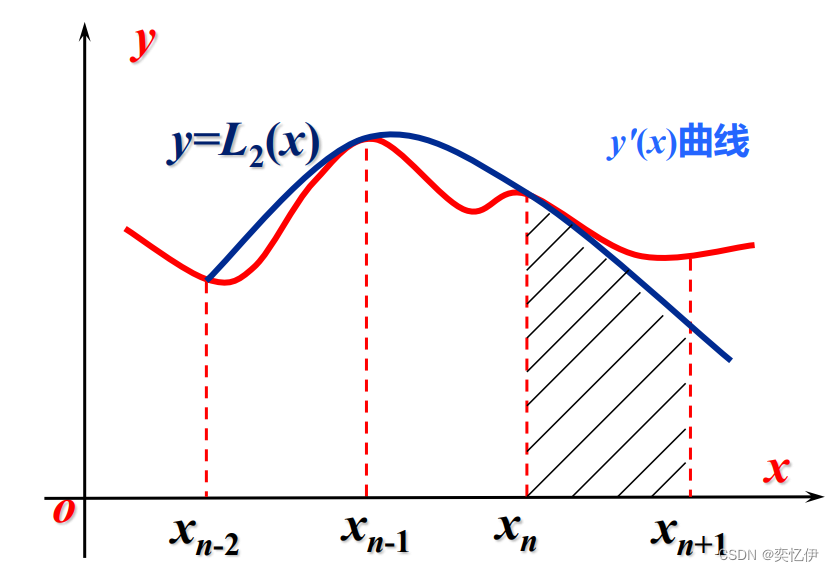
如果对xn-2、xn-1、xn、三点做二次拉格朗日插值多项式 L2 (x)近似取代y'(x),则有:
以此类推可以得到曲线的近似。
二阶隐式Adams公式,也就是梯形公式。
3.一阶常微分方程组的数值解法
4.高阶常微分方程的数值解法
三·MATLAB求解常微分方程
(一)解析解
1.dsolve
例3.1:
y=dsolve('D2y+4*Dy+29*y=0','y(0)=0,Dy(0)=15','x')
%结果 y = 3*sin(5*x)*exp(-2*x)
例3.2:
注:解微分方程组时,如果所给的输出个数与方程个数相同,则方程组的解按词典顺序输出;如果只给一个输出,则输出的是一个包含解的结构(structure)类型的数据。
%输出形式1:
[x,y,z]=dsolve('Dx=2*x-3*y+3*z','Dy=4*x-5*y+3*z','Dz=4*x-4*y+2*z','t')
%结果
%x = C1*exp(-t) + C3*exp(2*t)
%y = C1*exp(-t) + C2*exp(-2*t) + C3*exp(2*t)
%z = C2*exp(-2*t) + C3*exp(2*t)
%输出形式2
r=dsolve('Dx=2*x-3*y+3*z','Dy=4*x-5*y+3*z','Dz=4*x-4*y+2*z','t')
%结果2
%r =
%包含以下字段的 struct:
%y: C1*exp(-t) + C2*exp(-2*t) + C3*exp(2*t)
%x: C1*exp(-t) + C3*exp(2*t)
%z: C2*exp(-2*t) + C3*exp(2*t)
(二)数值解
事实上只有很少一部分微分方程能解出解析解。
多数情况下还是使用数值解的解法
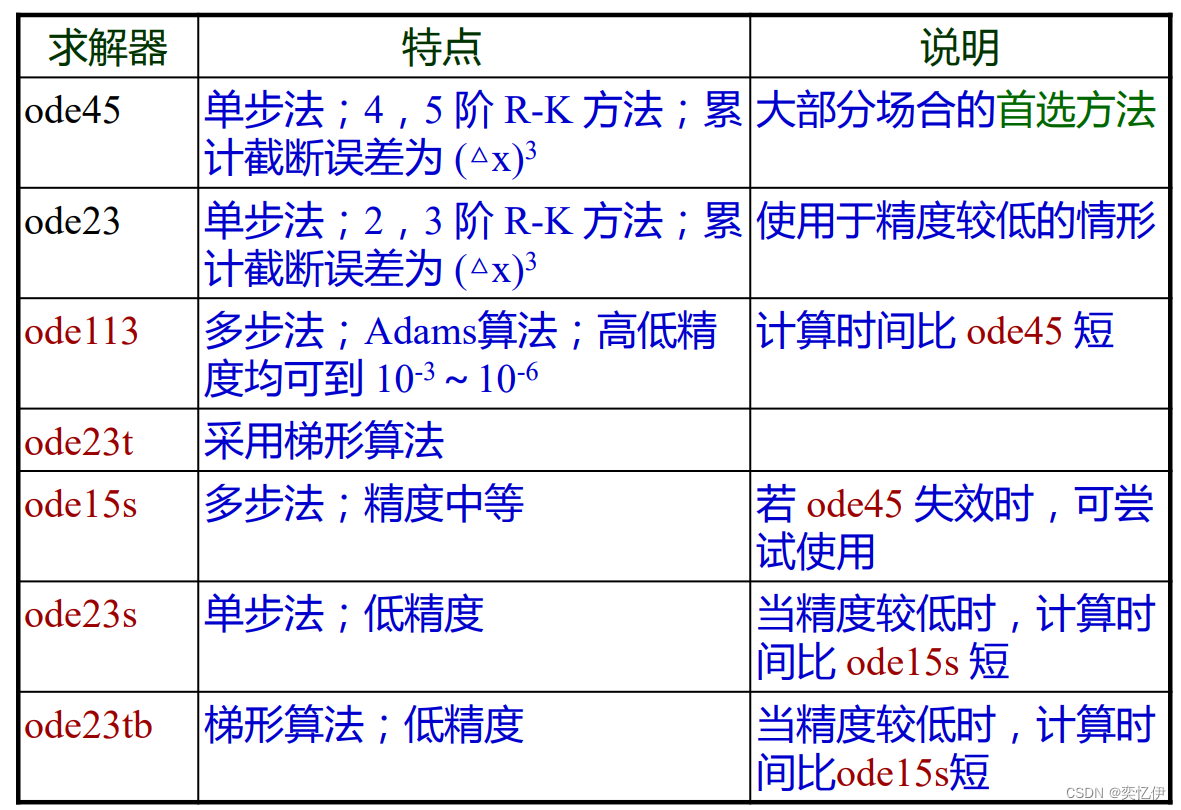
1.solver
关于求解器的对比:
若 odefun 为显式常微分方程,可以用命令 inline 定义,或在函数文件中定义,然后通过函数句柄调用。
例3.3:求下列微分方程的数值解,求解范围为 [0,0.5]
fun=inline('-2*y+2*x^2+2*x','x','y')
[x,y]=ode23(fun,[0,0.5],1)
%结果 fun =
%内联函数:
%fun(x,y) = -2*y+2*x^2+2*x
%x =[0 0.0400 0.0900 0.1400 0.1900 0.2400 0.2900 0.3400 0.3900 0.4400 0.4900 0.5000]
%y =[1.0000 0.9247 0.8434 0.7754 0.7199 0.6764 0.6440 0.6222 0.6105 0.6084 0.6154 0.6179]
%注:也可以在 tspan 中指定对求解区间的分割,如:
[x,y]=ode23(fun,[0:0.1:0.5],1); %此时 x=[0:0.1:0.5]
% x = [0 0.1000 0.2000 0.3000 0.4000 0.5000]
%y = [1.0000 0.8287 0.7103 0.6388 0.6093 0.6179]
2.高阶常微分方程
如果需求解的问题是高阶常微分方程,则需将其化为一阶常微分方程组, 此时需用函数文件来定义该常微分方程组。
例3.4:
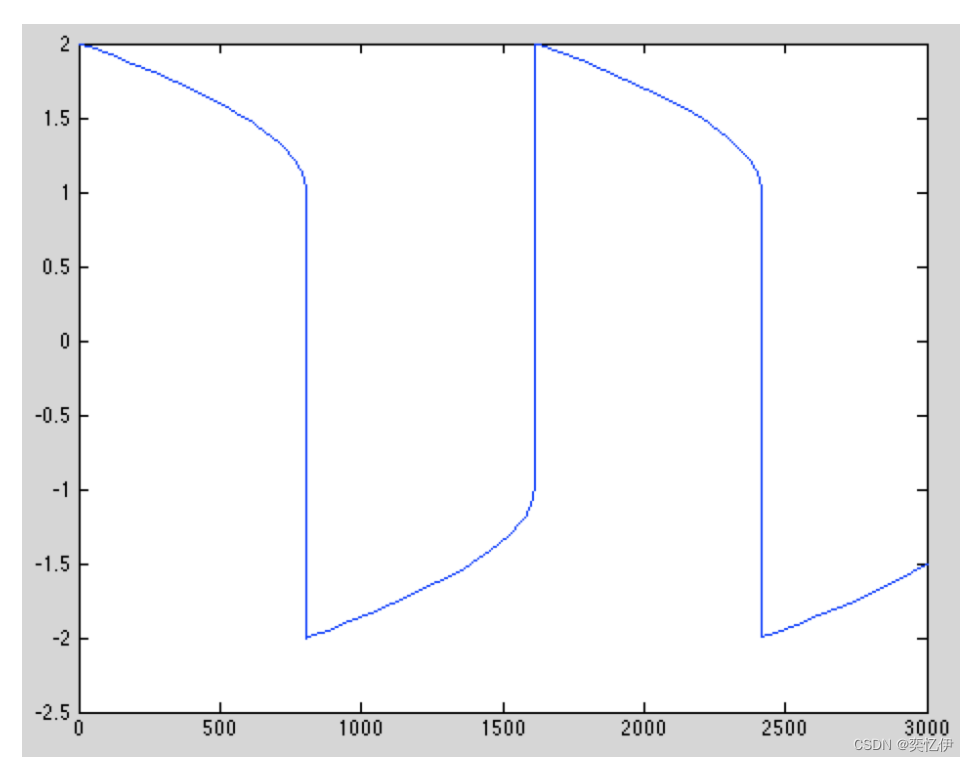
%先编写函数文件 vdp1000.m function dy=vdp1000(t,y) %定义函数vdp1000 dy=zeros(2,1); %2行1列列向量 dy(1)=y(2); dy(2)=1000*(1-y(1)^2)*y(2)-y(1);
%然后在命令窗口运行 clear; clc; [T,Y]=ode15s(‘vdp1000’,[0,3000],[2 0]); %调用ode15s求解vdp1000 plot(T,Y(:,1),‘-’); %Y=[y(1) y(2)],画出y(1)
(三)综合实例
求解下列微分方程:
1.一阶微分方程
(1)将方程写成函数文件
%fun1.m
function f=fun1(x,y)
f = sin(x)+y;
end
(2)解析解
y=dsolve('Dy=sin(x)+y','y(0)=1','x')
从输出得知,此方程有解析解,我们可以取一些x值带入解析解,求出y,然后画出精确的曲线
画出解析解的图形
%完整脚本
f=dsolve('Dy=sin(x)+y','y(0)=1','x')
X=0:0.1:3; %取[0,3]区间的值
n=length(X); %所取值的数量
df=zeros(1,n);%生成与x取值数量对应的y的数组
for i=1:n %写一个循环,把根据解析方程求得的y值放入数组df
temp=subs(f,'x',X(i)); %subs(方程,‘待取代的变量’,‘取代变量的实际值’)
df(i)=double(vpa(temp)); %把求得的y值转换为双精度,否则会因为运算强制取整
end
plot(X,df,'-k') %绘图
(3) 求解器法
使用MATLAB自带求解器求解
为了保证算法的通用性,后面都用函数文件的形式保存
%o45.m function o45(fun,t0,tm,y0) %(函数,自变量区间初值,自变量区间末值,y值初值) %命令窗口输入: %o45(@fun1,0,3,1) %@fun1是直接调用前面我们写好的函数文件中的函数 [t,y]=ode45(fun,[t0 tm],y0); plot(t,y,'-g') hold on %保留绘图窗口,下一次绘图也在这个窗口
(4)欧拉法
写代码的思路和手算例题的思路一致,确定f(x,y)的方程,步长,x的取值,然后按公式计算yk
只是多了一步,需要写一个保存yk的数组
%oula.m
function oula(f,h,xm,x0,y0)
% f切线方程 h步长 xf自变量最大值 x0,y0初值
%oula(@fun1,0.1,3,0,1)
x = [x0:h:xm];
% length函数是求数组维度的长度。
n = length(x);
%用数组y保存计算得到的yk值
y = zeros(1,n);
y(1) = y0;
for i= 1:n-1
y(i+1) = y(i) + h*f(x(i),y(i));
end
plot(x,y,'-m')
grid on
hold on
(5)改进欧拉法
%oulagai.m
function oulagai(f,h,xm,x0,y0)
% f切线方程 h步长 xf自变量最大值 x0,y0初值
%oulagai(@fun1,0.1,3,0,1)
x = [x0:h:xm];
n = length(x);
y = zeros(1,n);
y(1) = y0;
for i= 1:n-1
K1 = h*f(x(i),y(i));
K2 = h*f(x(i+1),y(i)+K1);
y(i+1) = y(i)+0.5*(K1+K2);
%下面是另外一种写法
%y(i+1)=y(i)+h*f(x(i),y(i));
%y(i+1)=y(i)+h/2*(f(x(i),y(i))+f(x(i+1),y(i+1)))
end
plot(x,y,'-b')
hold on
(6)龙格-库塔法
%longge.m
function longge(f,h,xm,x0,y0)
% f切线方程 h步长 xf自变量最大值 x0,y0初值
%longge(@fun1,0.1,3,0,1)
x = [x0:h:xm];
n = length(x);
y = zeros(size(x));
y(1) = y0;
for i= 1:n-1
K1 = f(x(i),y(i));
K2 = f(x(i)+0.5*h,y(i)+0.5*h*K1);
K3 = f(x(i)+0.5*h,y(i)+0.5*h*K2);
K4 = f(x(i)+h,y(i)+h*K3);
y(i+1) = y(i)+(h/6)*(K1+2*K2+2*K3+K4);
end
plot(x,y,'-r')
hold on
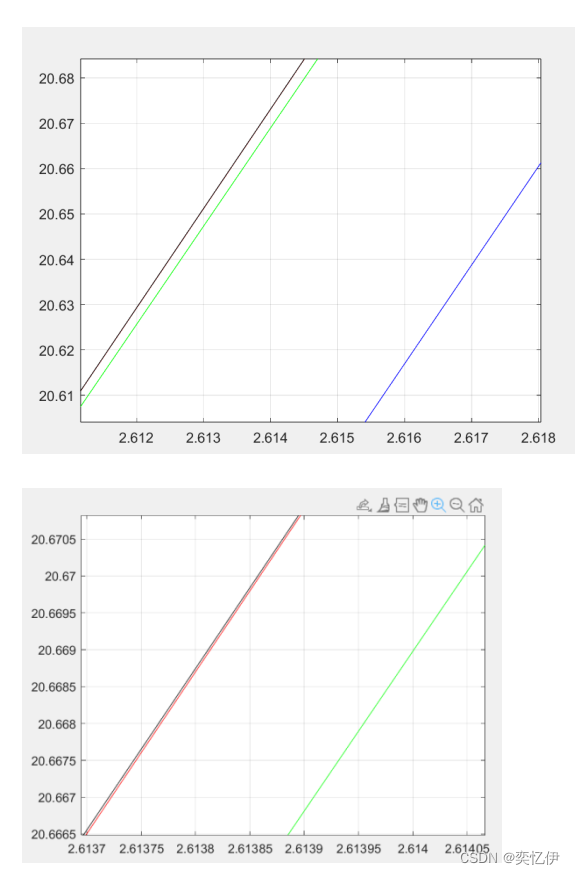
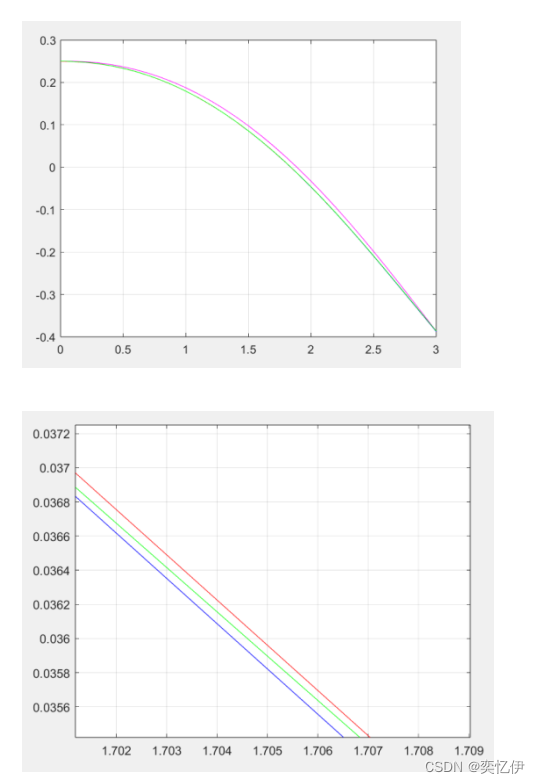
结果:
可见欧拉法的误差很大,逐渐放大看,改进欧拉法其次,四阶龙格库塔和 ode45 的误差相近。
2.二阶微分方程
首先就是把二阶化成一阶方程组
(1)把方程写成函数文件
%fun2.m
function F=fun2(t,Y)
y = Y(1);
z = Y(2);
f1 = z;
f2 = (-y-(-1+y^2)*z)/2;
F = [f1;f2];
end
f1和f2对应的是方程组的输出,用数组F保存
y和z是方程的两个输入,用数组Y保存
这样写,方便之后的循环迭代
(2)解析解
y=dsolve('2*D2y+(y^2-1)*Dy+y=0','y(0)=0.25','Dy(0)=0.0')
(3)欧拉法
%oular2.m
function oular2(fun,t0,y0,z0,h,tm)
%oular2(@fun2,0,0.25,0.0,0.1,3)
t=t0:h:tm;
n=length(t);
y(1)=y0;
z(1)=z0;
Y(:,1)=[y(1),z(1)];
for i = 1:n-1
Y(:,i+1)=Y(:,i)+h*fun(t(i),Y(:,i));
end
y=Y(1,:);
figure(2)
%黑色
plot(t,y,'-m')
hold on
grid on
(4)改进欧拉法
%oulargai2.m
function oulargai2(fun,t0,y0,z0,h,tm)
%oulargai2(@fun2,0,0.25,0.0,0.1,3)
t = [t0:h:tm];
n = length(t);
Y(:,1)=[y0,z0];
for i= 1:n-1
Y(:,i+1)=Y(:,i)+h*fun(t(i),Y(:,i));
Y(:,i+1)=Y(:,i)+h/2*(fun(t(i),Y(:,i))+fun(t(i+1),Y(:,i+1)))
end
y=Y(1,:);
%蓝色
plot(t,y,'-b')
hold on
(5)龙格-库塔法
%longge2.m
function longge2(fun,t0,y0,z0,h,tm)
%longge2(@fun2,0,0.25,0.0,0.1,3)
t = [t0:h:tm];
n = length(t);
Y(:,1)=[y0,z0];
for i= 1:n-1
K1 = fun(t(i),Y(:,i));
K2 = fun(t(i)+0.5*h,Y(:,i)+0.5*h*K1);
K3 = fun(t(i)+0.5*h,Y(:,i)+0.5*h*K2);
K4 = fun(t(i)+h,Y(:,i)+h*K3);
Y(:,i+1) = Y(:,i)+h/6*(K1+2*K2+2*K3+K4);
end
y=Y(1,:);
%红色
plot(t,y,'-r')
hold on
(6)求解器
%o452.m function o452(fun,t0,y0,z0,tm) %o452(@fun2,0,0.25,0.0,3) [t,y]=ode45(fun,[t0 tm],[y0 z0]); %绿色 plot(t,y(:,1),'-g') hold on


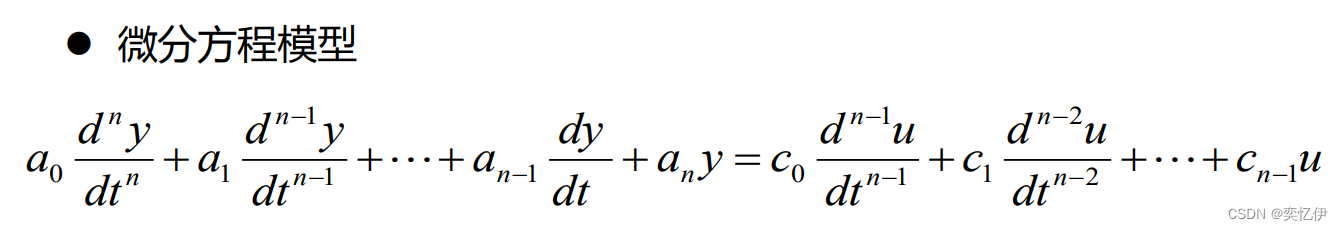

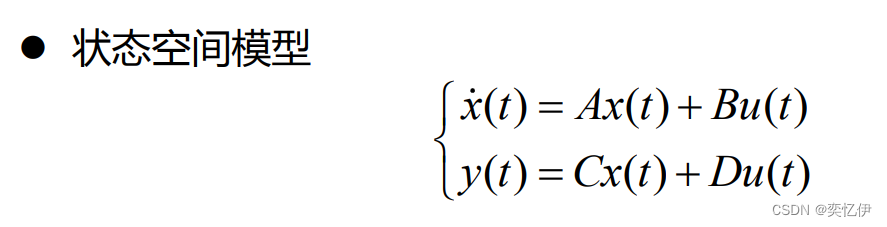

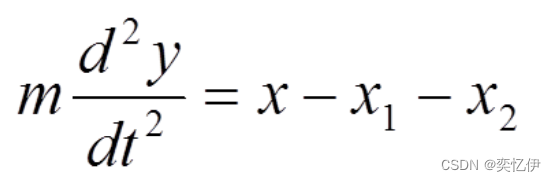
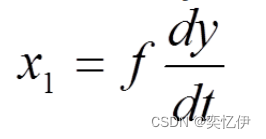
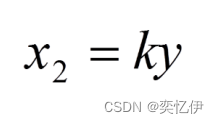
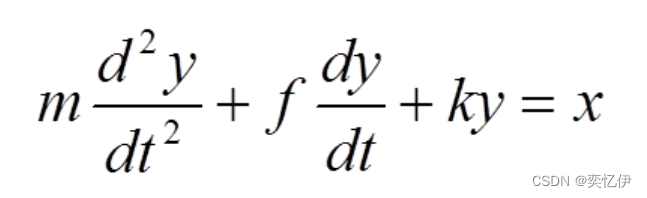
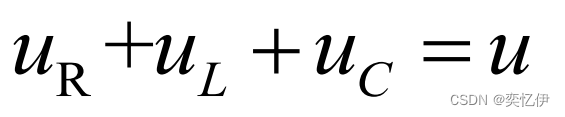

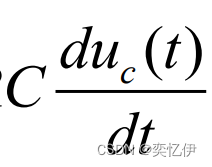
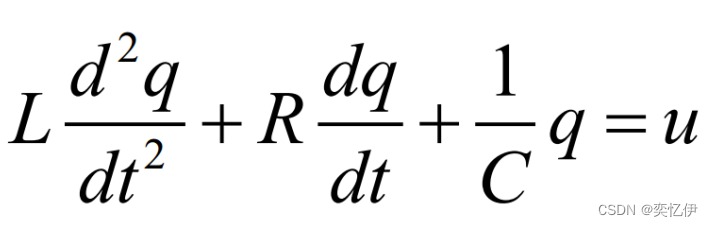





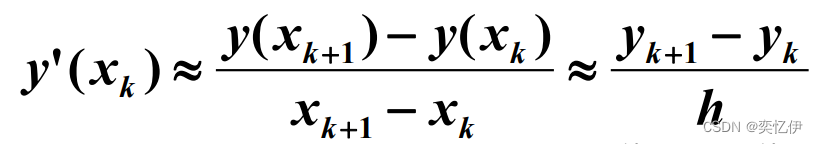
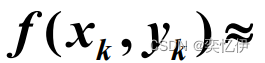
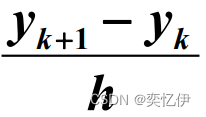

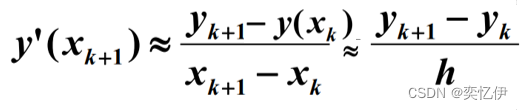
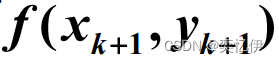
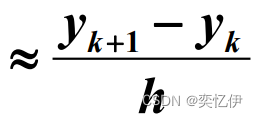
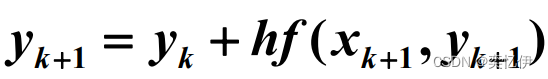
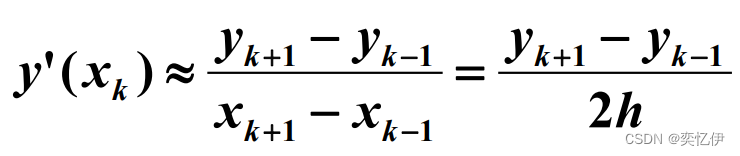
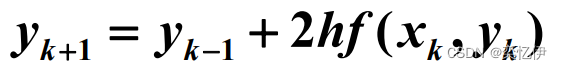




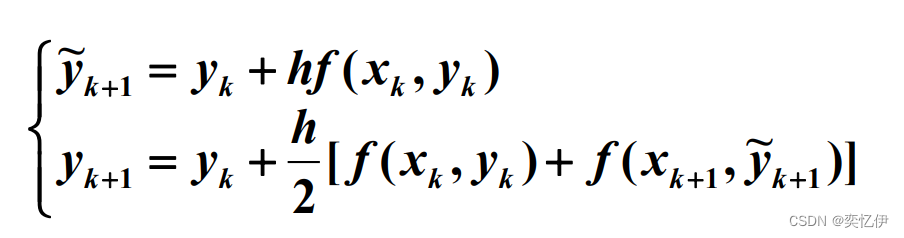
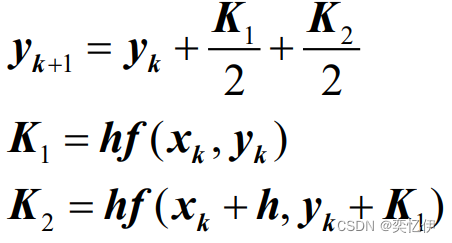






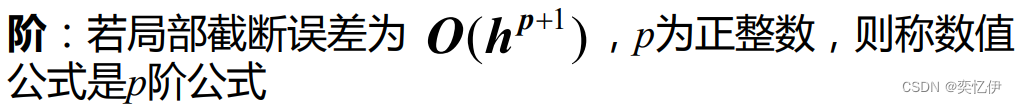








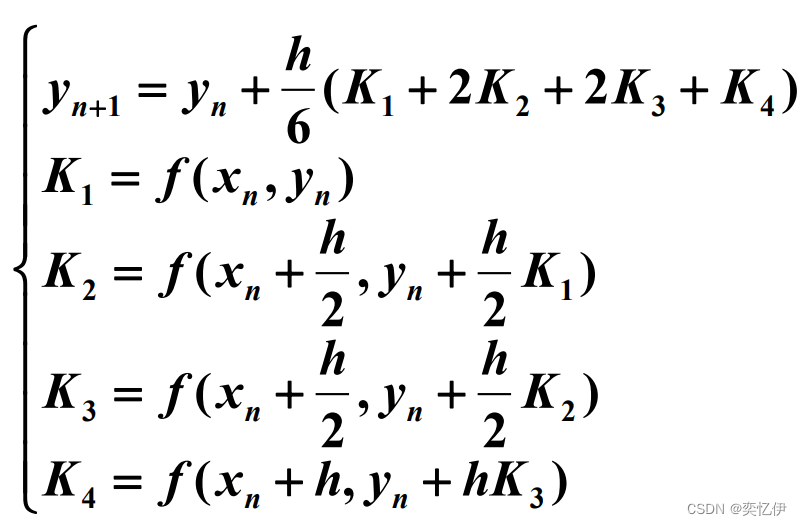



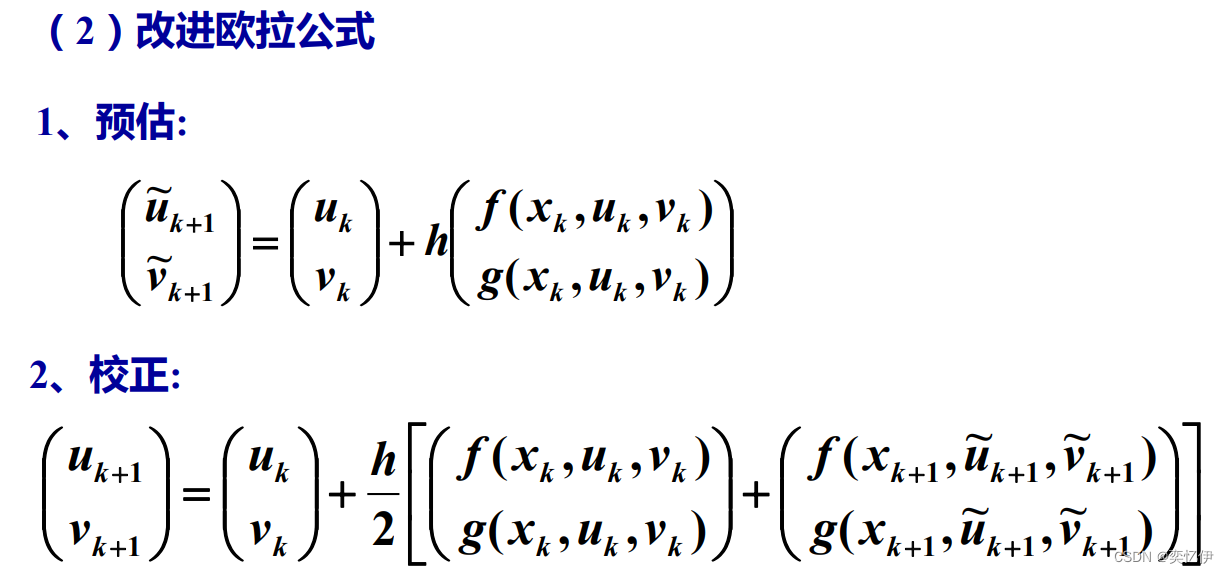







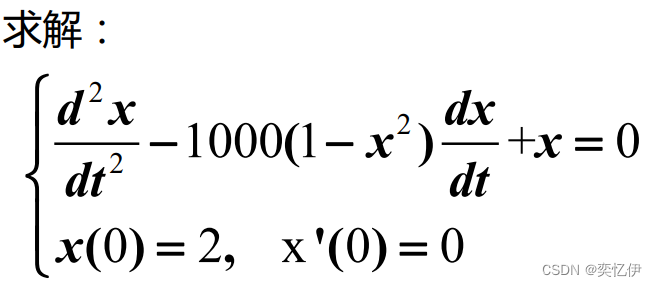
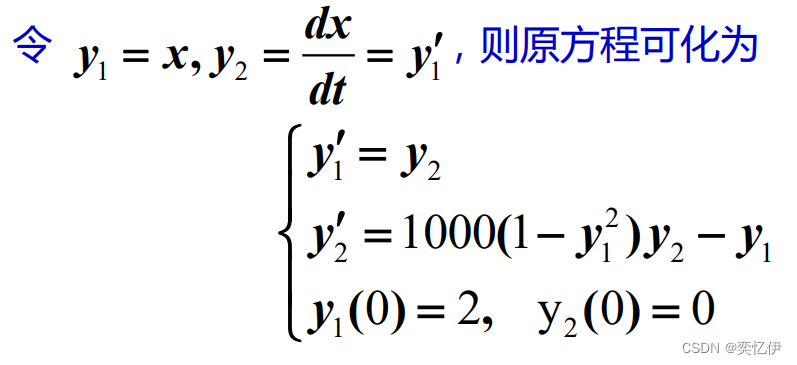

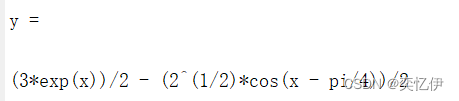


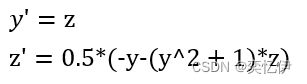





还没有评论,来说两句吧...